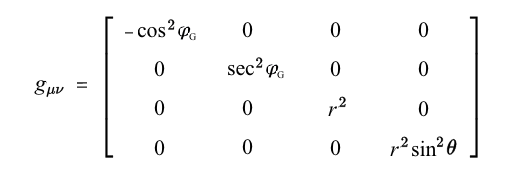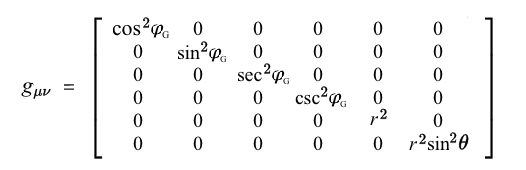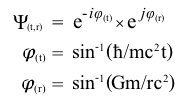Gravitational Phase
The gravitational phase angle defines four phase-states of spacetime according to their spatial energy density, with inter-phase boundaries at φG = π/2, π, 3π/2 and 2π. |
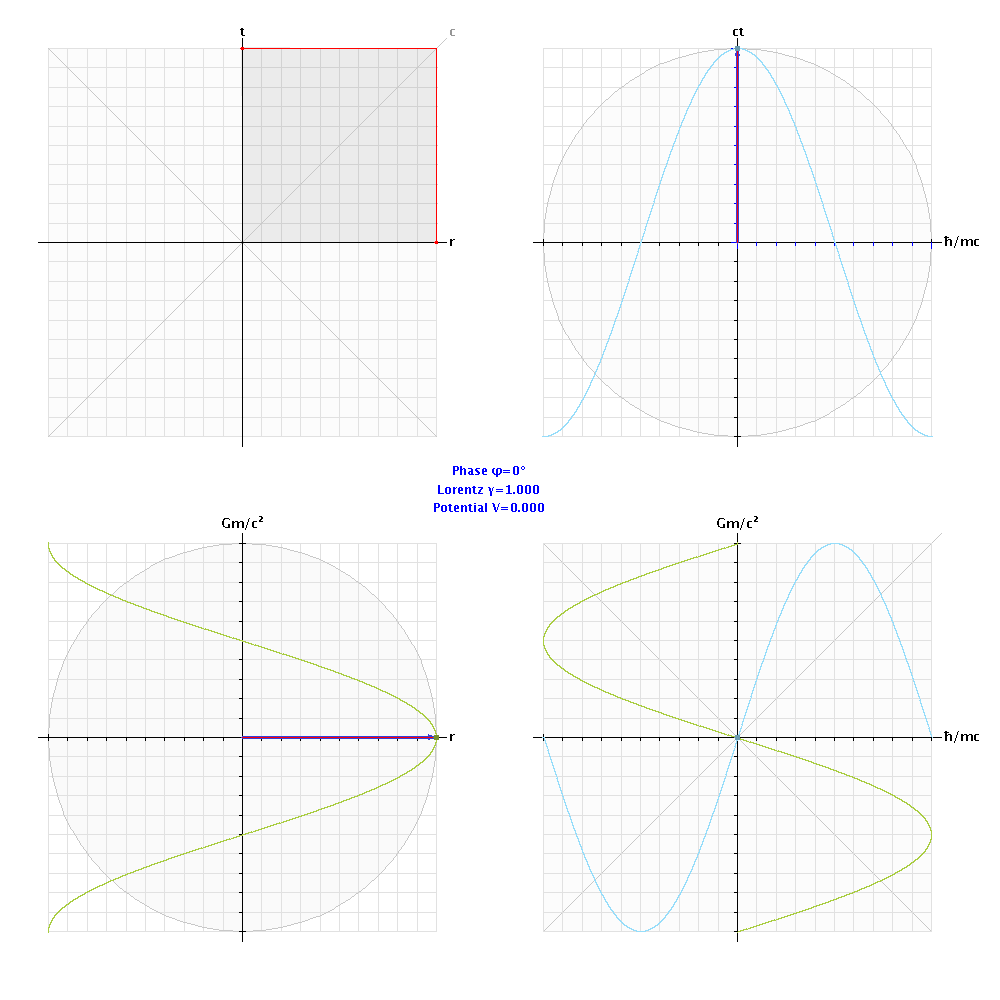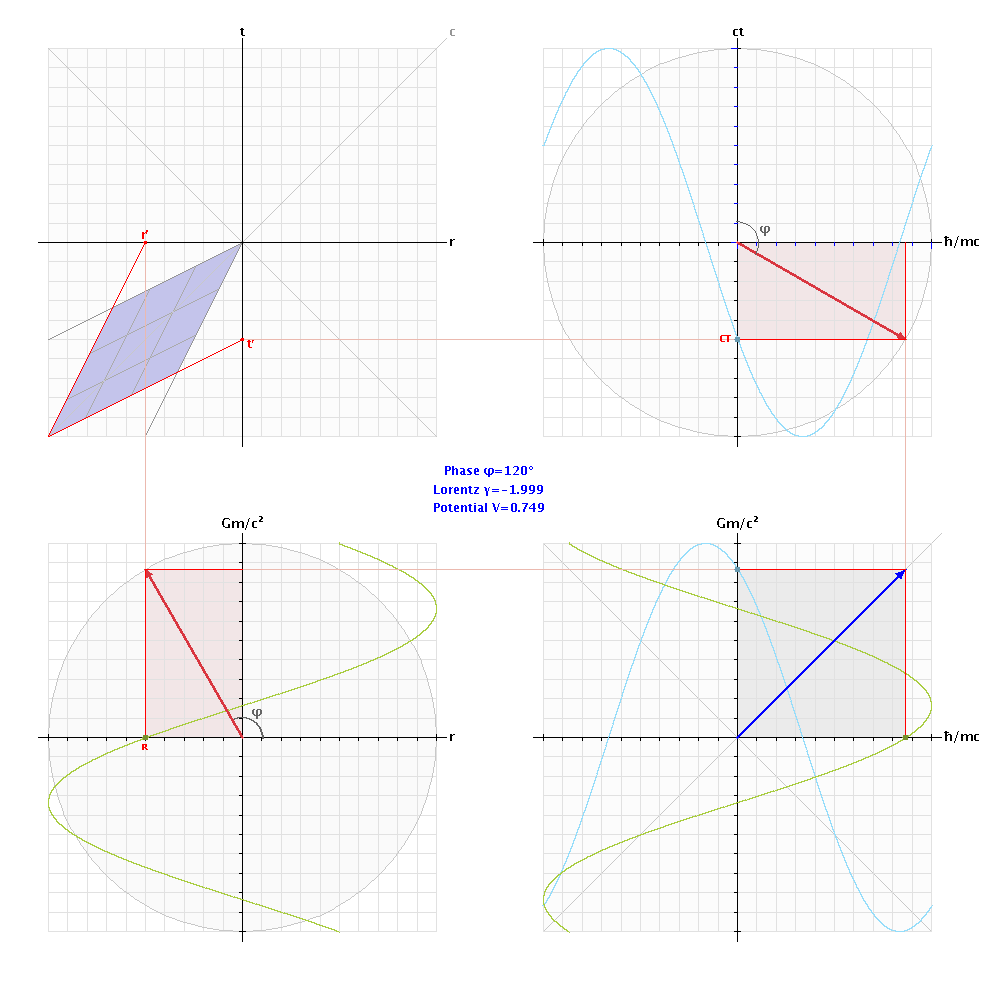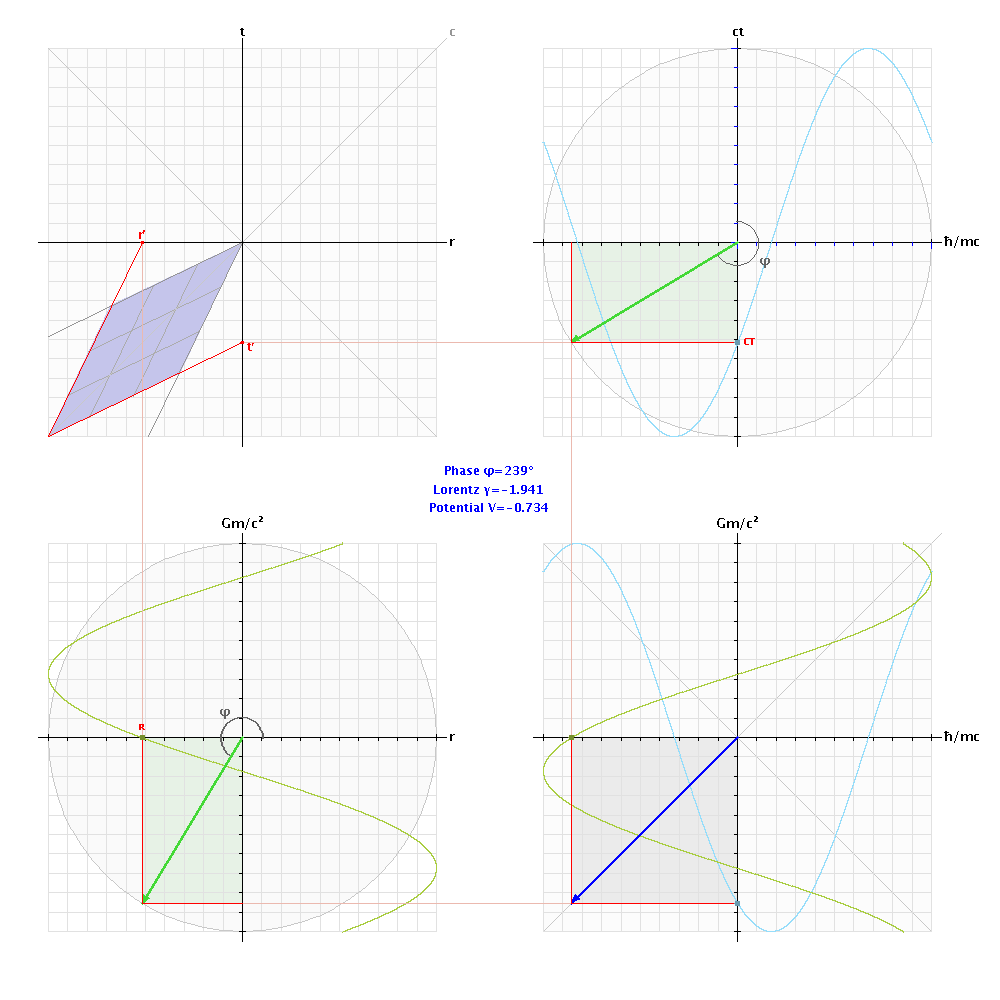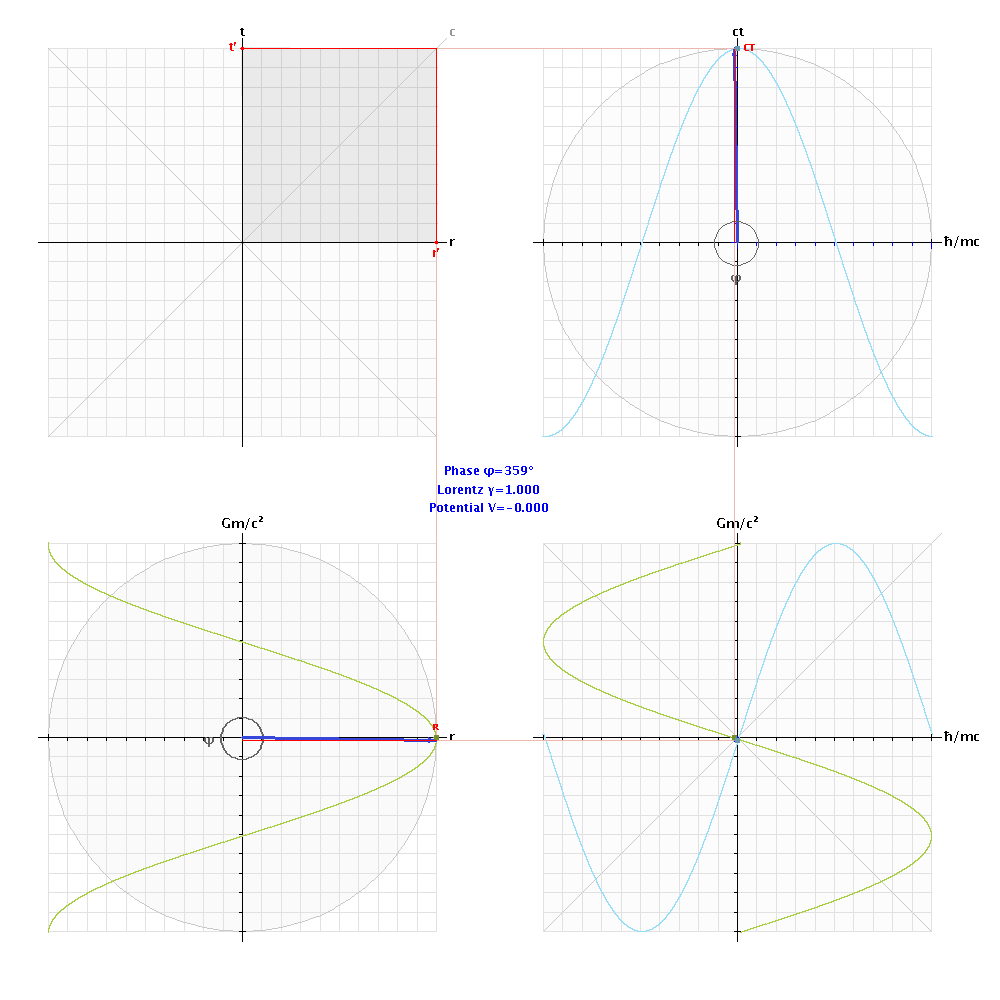
The Minkowski MetricIf space were a perfect vacuum, containing no matter or electromagnetic energy, the gravitational potential would be exactly zero at every point, so spacetime would be perfectly flat, with no gravitational curvature. This zero-gravity 3+1D spacetime is described by the Minkowski metric η, the components of which can be represented by a 4×4 matrix in the coordinates ct,x,y,z: Irrespective of the velocity of an observer, the 4-dimensional distance separating any two points (events) in Minkowski spacetime is given by the invariant line element Δs, where: For a ray of light propagating in the x direction, the line interval Δs is zero, since Δct = Δx. Thus, on its null world-line, the speed of light is constant in any inertial frame of reference and coordinate system. The Schwarzschild MetricIn general relativity, the Newtonian (scalar) gravitational potential VG = GM/r is replaced by a metric tensor gμν (where μ,ν = 0,1,2,3), e.g. the Schwarzschild metric in polar coordinates (ct,r,θ,φ), which can be formulated in terms of the gravitational phase angle φG = sin-1√(2GM/rc2) as follows: The Schwarzschild metric gμν describes a static uncharged black hole in an empty vacuum. It determines the invariant square of an infinitesimal spacetime interval (4D distance), the line element ds2: where t is coordinate time, r is the spatial distance separating the events, and Ω is the solid angle in spherical coordinates, where dΩ2 = dθ2 + sin2θ⋅dφ2. The 4-dimensional Schwarzschild metric only applies to regions of space external to a black hole’s event horizon, i.e. where r is greater than the Schwarzschild radius Rs = 2GM/c2. This event horizon represents the spherical surface where the escape velocity equals the speed of light (ve/c = 1), and the gravitational phase angle φG equals π/2. A metric pertaining to the interior of a black hole, describing regions of spacetime inside its event horizon, where the gravitational phase angle exceeds π/2, requires two further degrees of geometric freedom to eliminate an un-physical 4D singularity at r = 0. Accordingly, the Schwarzschild metric gμν can be formulated as a six-dimensional matrix in the quaternionic spherical coordinates (ict, jℏ/mc, r, kGm/c2, θ, φ) where i,j,k = √-1 and μ,ν = (0,1,2,3,4,5): Setting the solid angle dΩ to zero, the 6x6 metric on this complex Kähler manifold determines an invariant line element (6D distance): The Gravitational Phase FunctionOn this spacetime metric with 6 degrees of freedom, an equation describing time dilation and spatial contraction as a function of mass-energy density can be obtained, revealing a 6D function which takes the form of two orthogonal phase vectors (phasors): where φ(t) is the temporal phase angle given by cos-1(dt'/dt), φ(r) is the spatial phase angle given by cos-1(dr'/dr), and i,j = √-1. The primed quantities t' and r' are the proper time and proper length in the gravitating frame of reference. The gravitational phase equation can be visualised by employing geometric projections of the imaginary coordinate axes ict, jℏ/mc, and kGm/c2 against a Minkowski diagram of spacetime's “4D-rotation”. The following animation simulates increasing the mass-energy density (from zero to Planck density) within a fixed volume of space, and reveals the behaviour of the spatial and temporal phasors over the 6-dimensional complex metric: |
|
The area representing the cross product of the temporal and spatial phase vectors (bottom-right) is given by sin2φ, and is therefore proportional to the gravitational potential VG = c2⋅sin2φ (J/kg), a scalar proxy for spacetime curvature. As the energy density reaches 0.239 Planck density (1.105 × 10113 J/m3), the gravitational phase angles reach π/2. This equates to the event horizon of a black hole, where escape velocity equals the speed of light. As density increases further, spacetime is inverted (mirrored relative to an observer in the zero-gravity rest frame), so a clock in the region inside the event horizon of a black hole goes backwards relative to coordinate time, and a ruler measures negative distances. Thus, the speed of light remains invariant.
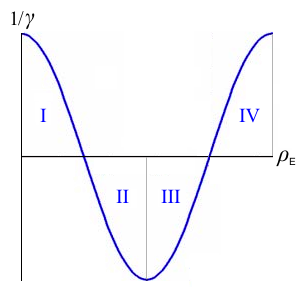
When the gravitational phase reaches π radians, the gravitational potential VG goes to zero. As density increases further, the potential becomes negative (spacetime's curvature inverts), equivalent to “anti-gravity” relative to our inertial observational frame. When the phase angles reach 3π/2, spacetime becomes positive once again, so clocks begin ticking clockwise. This inner event horizon within the high-density core of the black hole is exactly equivalent to a “white hole” (time-reversed black hole) such as is hypothesised to exist at the origin of our universe, time-zero of the Big Bang. Phase-States Of SpacetimeThe fabric of spacetime has 4 distinct phases, analogous to matter having 4 states (solid, liquid, gaseous and plasma) in accordance with its internal energy, i.e. temperature and pressure. The 4 phase-states of spacetime (Penrose regions), designated PI, PII, PIII and PIV, are correlated with the spatial energy density ρE. Relative to coordinate time t, as measured by a stationary clock in the CMB rest frame, two of spacetime's phase-states (PI and PIV) are characterised by forward-time and positive gravitational curvature, the other two (PII and PIII) by reverse-time and negative curvature. An event horizon is the boundary between positive and negative phase-states (curvature) of spacetime. A black hole's event horizon occurs at the conformal boundary between PI and PII, where the gravitational phase angle reaches π/2. A white hole's event horizon occurs (in inverted spacetime) at the boundary between PIII and PIV, where the gravitational phase angle goes through 3π/2. The PI region represents the “weak gravity” space exterior to a black hole's event horizon. The PII, PIII and PIV phase-state regions are interior to the event horizon, as energy density within the black hole increases exponentially towards its core. Thus, at the heart of an ancient ultra-massive black hole, within the PIV region of spacetime, instead of an impossible infinite-density singularity where “the laws of physics break down”, might lie another entire universe... “The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.” ~ Hermann Minkowski |