

James Clerk Maxwell, the father of dimensional analysis, declared length, time and mass to be "The Three Fundamental Units" of all the other significant physical quantities, such as velocity, acceleration, momentum, force and energy. However, he pointedly noted that while spatial length [L] and clock time [T] are fundamentally irreducible dimensions, the units of gravitational mass [Mg] can in fact be derived as [L3/T2]. This peculiarity must have intrigued and puzzled him, but he didn't elaborate on his discovery any further.

Maxwell, JC: "A Treatise on Electricity and Magnetism", 1873, p4
Later in the Treatise, he defined the unit of electrical charge (Q) as having dimensions of √([M∙L3/T2]), which classical physics defines as the Coulomb, i.e. a certain quantity of charged particles. By simply substituting Maxwell's length/time dimensions for gravitational mass into Q2, then taking the square root of the result, it is immediately obvious that charge has the same fundamental dimensionality as mass, namely [L3/T2].
Therefore both mass and charge are derived quantities, i.e. neither is intrinsically fundamental, as implied by the SI base units of kilograms, coulombs and amperes used in traditional dimensional analysis. Mass and electrical charge appear to be emergent quantities, themselves derived from the more fundamental dimensions of length [L] and time [T].
By substituting Maxwell's dimensions for mass (and charge) into the classical dimensions of the Planck Units, a number of intriguing patterns emerge. Trivially, spatial length is [L], surface area has dimensions of [L2], and volume is [L3]. Velocity has dimensions of [L/T] and acceleration is [L/T2]. Mass and electrical charge are now defined by their Maxwellian dimensions of [L3/T2], rather than the classical [M] and [Q].
The first surprise is voltage (V), aka electrical potential (EMF): this quantity has dimensions of [L2/T2]; its Planck Unit definition is a function of c2, the speed of light squared. Then there's electrical current (I), classically measured in amperes, which now has dimensions of [L3/T3] and a Planck Unit (classically in Coulombs per second) defined as a function of c3.

Force (F) has dimensions of [L4/T4], and the Planck unit of force is a simple function of c4 divided by G, Newton's gravitational constant (which is now dimensionless). Finally, there's power (P), classically measured in Watts or Joules/second, whose Maxwellian dimensions are [L5/T5]. The Planck unit of power (Pp) is given by c5/G.
This set of quantities lies on the diagonal of a 5x5 matrix, constructed with the five sequential powers of time [T] along its columns, and powers of length [L] down its rows. For completeness, we also include an origin point where the dimensionless constants are represented, viz. [L0/T0]. Thus, a 6x6 matrix may be constructed, as follows:
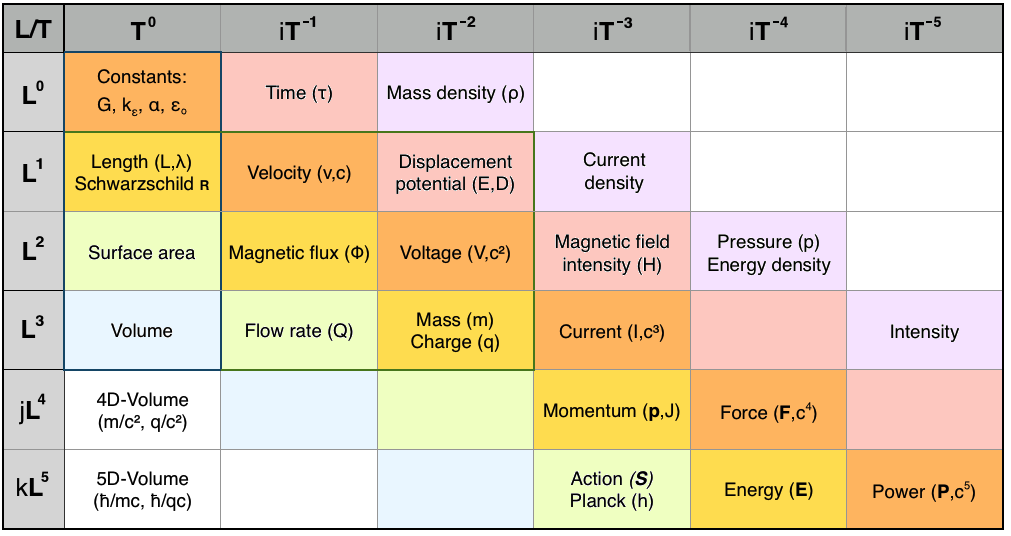
It is immediately obvious that this Maxwellian dimensional analysis represents a space-time having a total of six dimensions, five of spatial length plus one dimension of time. Three of the spatial dimensions are the real x,y,z dimensions of Euclidean space: length, breadth and height. However, the other three dimensions must be mathematically imaginary, i.e. the result of a Wick-rotation (by π/2) into an orthogonal imaginary dimension having units of length. They exist, like time, in another dimension, but we can't directly see them, nor move around in them. They're invisible to us, like the electromagnetic and gravitational "potentials" whereby Nature mysteriously stores energy in spacetime itself.
"The peculiarity of our space is that of its three dimensions, none is before or after another. As is x, so is y, and so is z. If you have 4 dimensions, this becomes a puzzle. For first, if three of them are in our space, then which three? Also, if we lived in space of m dimensions, but were only capable of thinking n of them, then first, which n? Second, if so, things would happen requiring the rest to explain them, and so we should either be stultified or made wiser. I am quite sure that the kind of continuity [spacetime] which has four dimensions all co-equal, is not to be discovered by merely generalising Cartesian space equations. ... it was Jacob Steiner who considered the final cause of space to be the suggestion of new forms of continuity." — James Clerk Maxwell, in correspondence with C.J. Monro, Esq., 15 Mar 1871
Maxwell's informal conversations with other mathematical physicists on the question of detecting additional dimensions clearly reveals he was trying to comprehend the orthogonal dimensionality of electric and magnetic "lines of force". His keen interest in understanding and utilising imaginary dimensions was also evident, for example: "I am getting converted to Quaternions, and have put some in my book [A Treatise on Electricity and Magnetism, 1873], in a heretical form..." — James Clerk Maxwell, correspondence with Prof. Lewis Campbell, 19 Oct 1872.
In his theory of Special Relativity (1905), Albert Einstein multiplied clock time by the speed of light (c) and the square root of minus one, the imaginary unit √-1, to construct an "imaginary time" dimension with units of length. In the ground-breaking "Electrodynamics of Moving Bodies" paper of 1905, Einstein explicitly defined the fourth spacetime dimension as √-1∙c∙t, or ict. This invention was necessitated by the phenomena of relativistic length contraction and time dilation, where a particle moving at a velocity close to the speed of light experiences time flowing at a slower rate, and distances shortening in the line of motion, as measured by an observer in an "inertial frame of reference", i.e. at rest. Einstein postulated "The Principle of Invariant Light Speed", meaning that light always travels at the same speed, c, irrespective of the relative motion of the light source and observer.

By 1907, however, Hermann Minkowski (his former mathematics tutor) had convinced Einstein that the √-1 imaginary unit was superfluous to his abstracted "geometrical four-dimensional spacetime manifold", subsequently known as Minkowski space. Instead of being a mathematically-imaginary dimension, time became a "pseudo-real" dimension in Einstein's General Theory of Relativity of 1915. Subsequently, Einstein only referred sporadically to the imaginary aspect of time, seemingly uncomfortable with an "imaginary quantity" that wasn't ponderable, material, and empirically measurable. He much preferred clocks, rulers, and trains.
Following Einstein's earlier instincts, the other two requisite dimensions of length may be defined along additional imaginary axes, via further multiplication by √-1. The quaternion calculus, which fascinated Maxwell, readily defines the requisite complex spacetime dimensions as Ζ = r(x,y,z) + iτ + jʀ + kλ. This quaternion notation encapsulates five dimensions of length (two of which are imaginary), plus an imaginary dimension of local (proper) time.
In the early 1920's, the mathematician Theodor Kaluza sent Einstein a paper describing a five-dimensional spacetime, showing that an additional spatial dimension could unify the disparate field theories of gravitation and electromagnetism. Einstein was deeply fascinated by Kaluza's 5D theory, but he was never comfortable with the idea of space having another dimension, since there's no experimental evidence for a fourth spatial dimension. However, if Kaluza's extra dimension is conceived of as imaginary (i.e. invisible) rather than compactified, the 5-dimensional complex version of Einstein's equations are mathematically robust.
In 2006, physicist Paul Wesson published "Five-Dimensional Physics: Classical and Quantum Consequences of Kaluza-Klein Cosmology", in which he identified two candidates for Kaluza's extra spatial dimension. Wesson showed that a "Planck gauge" could be derived from the equation for the Compton wavelength, λ = ħ/mc. He also identified an alternative metrical dimension, the "Einstein gauge", derived from the equation for the Schwarzschild radius, ʀ = 2Gm/c². Wesson's 5D spacetime metric incorporated both of these gauge definitions, swapping between them via a basis-coordinate transform.
However, Wesson's two "Planck" and "Einstein" gauges can more easily be applied to the fourth and fifth spatial dimensions demanded by Maxwellian 5+1 dimensional analysis, and thus, a complex 6-dimensional spacetime can be fully developed:
The quaternion notation, wherein ijk = i² = j² = k² ≡ −1, simply signifies that each dimension, real or imaginary, is mathematically orthogonal to all the others. It's equally valid to conceptualise a Euclidean 3D space in which each of the real x,y,z spatial dimensions is actually complex. In a classical Hilbert space, spatial extension (the quantity of distance) has both a real and an imaginary component, akin to the complex multi-dimensional configuration space of quantum eiφ wavefunctions, e.g. de Broglie's matter wave and Dirac's equation.
Normally, we only encounter the real aspect of spatial distance. The imaginary part only becomes evident at relativistic velocities (not your everyday experience), and in powerful gravitational fields (you're normally unlikely to land on a neutron star, or fall into a black hole). The only
After decades of studying electromagnetics, Maxwell was deeply fascinated by the question of "what's the particular go" of how potential energy is stored in space itself, i.e. in empty vacuum. He conceptualised a luminiferous æther, an invisible, elastic, insubstantial substance filling the entire volume of space, through which medium electromagnetic ripples could propagate. His calculations indicated that the æther contained a vast quantity of potential energy, which (for unknown reasons) diminished in the vicinity of mass, thereby causing gravity.
Maxwell's mathematical genius and instinct for physics led him to "convert" to using quaternion calculus, insisting that vector and tensor algebras were incapable of fully describing electromagnetic and gravitational phenomena. A quaternion is a complex mathematical object, encapsulating a scalar variable plus three orthogonal imaginary quantities, Z = a + ib + jc + kd. The "heretical form" of his quaternion calculations was to deliberately separate the scalar real (Euclidean space) from the imaginary three-tuple, giving no reason, but hinting at some deep insight into the fundamental geometry of spacetime.
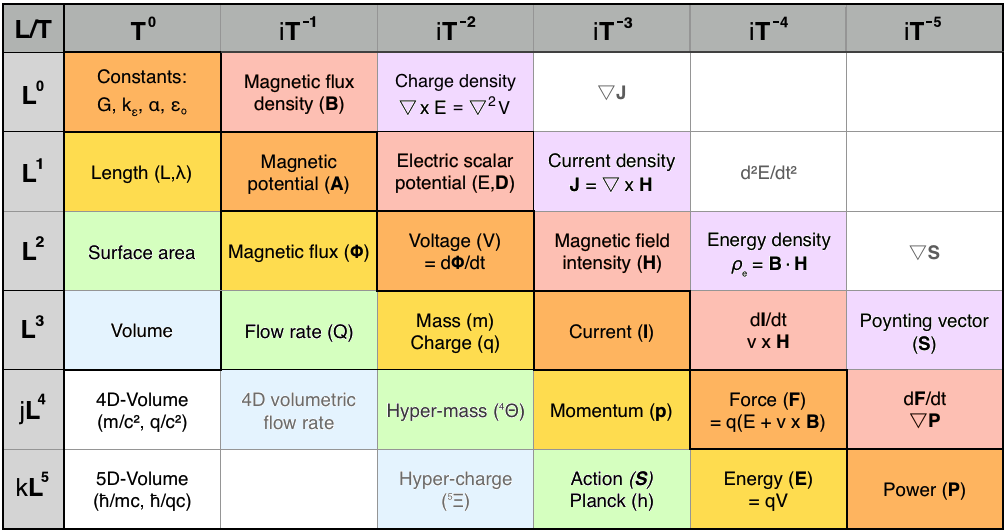
Unfortunately, very few physicists understood Maxwell's unconventional quaternion notation, which split their real and imaginary components. His publisher urged him to simplify the math, so he spent years revising his masterwork. Even that considerable simplification wasn't enough for the "Maxwellians", notably Oliver Heaviside, who reformulated Maxwell's field equations in terms of energy flux and electromagnetic forces. In the process, Heaviside naively eliminated the electric and magnetic potentials, which he considered "mystical" and "metaphysical". Fortunately, these potentials were eventually rescued from oblivion by Richard Feyman in his theory of Quantum Electrodynamics (QED).
Maxwell's unorthodox approach to quaternion calculus suggests that he'd intuitively grasped the notion of three orthogonal imaginary dimensions, superimposed on three orthogonal real dimensions. Nevertheless, he struggled to understand the means by which potential energy is stored in electromagnetic and gravitational force-fields, and how energy can impose stress into empty space itself, creating a magnetic tension, an electrical potential, or a gravitational field.

Max Planck, a German theoretical physicist, originated quantum theory in 1900 as "an act of despair" while trying to solve the problem of black-body radiation. The Planck Quantum of Action (h) is a fundamental constant with dimensions of [L5/T3], which relates the speed of light and the unit of inverse-length to the energy unit, dimensioned as [L5/T4], via the "Planck–Einstein" equation E = hc/λ.
This relation defines a quantum as the minimum quantity of energy required to form an electromagnetic field. A photon with Compton wavelength λ is the quantum of light with energy E = hf (where its frequency f = c/λ). A massive particle or "matter wave" having linear momentum of p has a de Broglie wavelength given by λ = h/p. Planck's coupling constant (h) enabled the definition of a set of natural physical units, based on the Planck length and Planck time, which form the theoretical foundations of modern quantum physics: the Planck Units.

Originally, the Planck Units were defined in terms of the fundamental quantities of spatial length [L], time [T], mass [M] and charge [Q]. Thereby, the natural coupling constants of classical physics such as Newton's gravitational constant (G), the speed of light (c), the Coulomb constant (ke), and Planck's constant itself (h) were all "normalised" to unity.
By refactoring the units of mass and charge into units of length and inverse-time, per Maxwell's [M] = [L3/T2], we flatten the many-dimensional configuration space of the original Planck Units into a simple 2D matrix, bounded by the two canonical dimensions of spacetime: [L] and [T]. This simplification permits a deep analysis of the Planck Units in terms of a few simple rules of matrix calculus: to descend any column, multiply by the unit of length; to increment along a row, multiply by the unit of inverse-time; to move down-right along any diagonal, multiply by the speed of light (c).
To differentiate a quantity with respect to time (d/dt), we move one cell to the right, e.g. dp/dt = F [momentum → force]. To integrate the unit quantity over time, we slide to the cell on its left, e.g. ∫v∙dt = r [velocity → distance]. For differentiation with respect to space (d/dr), we move one cell upwards in the matrix, e.g. dp/dr = I [momentum → mass current]. Conversely, to integrate something over space, we drop down one cell, e.g. ∫F∙dr = E [force → energy].
The diagonal of this matrix lies along a logarithmic determinant measured in powers of c, the speed of light. The integral of these π/4 cardinal cells over space, ∫cndr, are Planck Units defined as a function of the square root of light-speed (c) and Planck's constant (h). Each alternate diagonal in the matrix, top-left to bottom-right, and top-right to bottom-left, follows the same pattern.
Although dimensionless, Newton's gravitational constant (G) hinges on the same diagonal axis as h, orthogonal to the determinant diagonal (powers of c). On this "Planck-Newton" diagonal, an intriguing new Planck Unit appears, with dimensions of [L4/T2]. Mathematically, this imaginary unit is the integral over space of momentum, the integral with respect to time of mass, and the canonical Planck quantity equals the Planck Action (h) divided by the speed of light (c).
This so-far undetectable quantity is the second differential in time (d2/dt2) of the imaginary unit length with dimensions [L4], the base component of the "Einstein gauge" given by ʀ = jGm/c². It can best be understood as "4D hypermass", from which gravitating matter emerges holographically in our three real spatial dimensions.
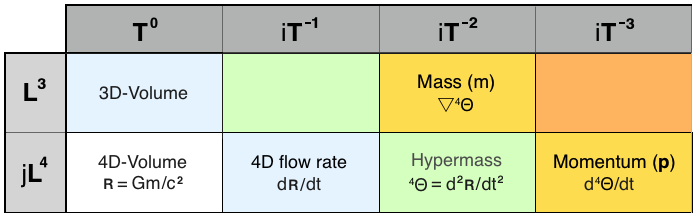
Of greater significance, hypermass can be defined as a function of gravitational force [L4/T4] divided by mass-density [1/T2], in SI units of m4/s2, and equivalently, of potential energy [L5/T4] divided by the gravitational field intensity [L/T2].
To validate the 5+1 dimensional spacetime model, it must be fully compatible with existing robust and well-verified theories of spacetime, electromagnetism and gravity. To that purpose, a graphical simulation of an uncharged particle (e.g. Planck mass) being accelerated to light-speed verifies that time dilation and Lorentz length contraction occur precisely as predicted by Special Relativity.
The 6D simulator determines that Planck force (1.21 x 1044 N) is required to accelerate Planck mass (2.176 x 10-8 kg) to light-speed, at which velocity it has acquired the Planck unit of momentum (6.525 kg∙m/s), which is equivalent to the Planck unit of energy (1.956 x 109 J). No surprises there, then. What is interesting, however, are the simulation's predictions regarding the de Broglie (momentum) wave-function: in the massive wavicle's direction of motion (x), its wavefunction has zero extension, but its radius in the orthogonal y,z dimensions tends to infinity. Luckily, a frame of reference moving at light-speed, in maximally-curved spacetime, becomes totally imaginary.
The simulation displays a simplified Minkowski diagram at top-left. As the test particle is accelerated, the "4D rotation" or "spacetime curvature" of the moving frame of reference can be clearly visualised, as the speeding particle's reference frame appears to twist 90° to the plane of the rest-frame, then completely disappear into imaginary spacetime. At this point, the speed of light, time is infinitely dilated (the particle's clock has stopped), and space is infinitely contracted (the particle's measuring-rod has shrunk to zero), as observed from the classical laboratory's inertial rest-frame.
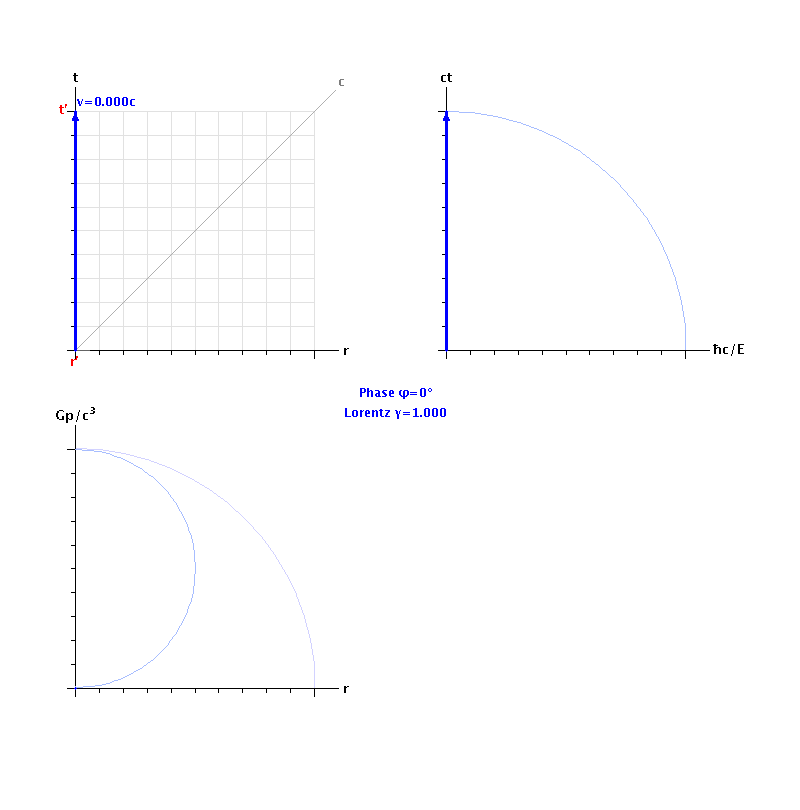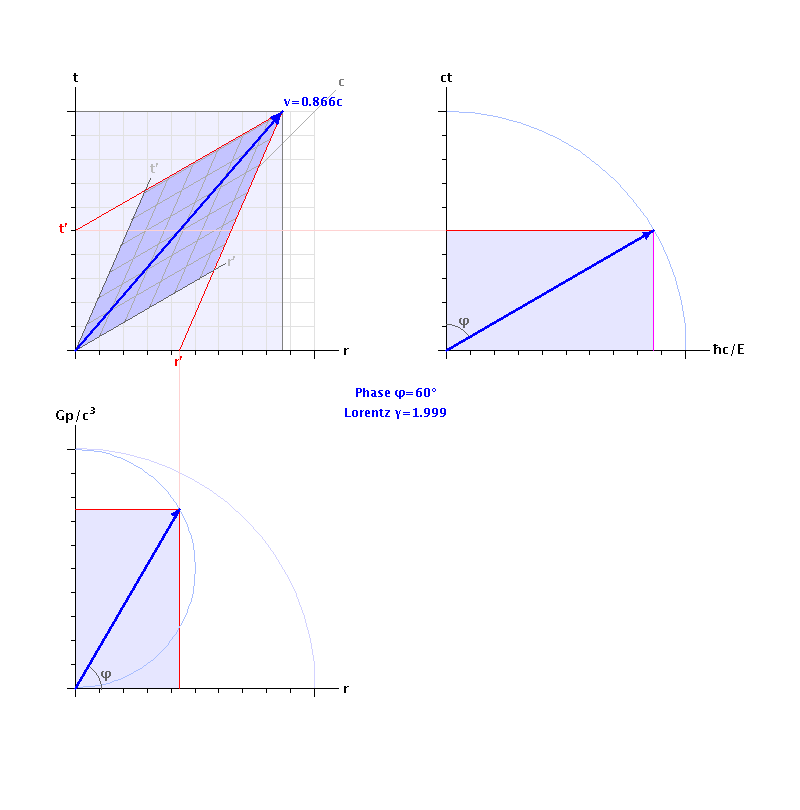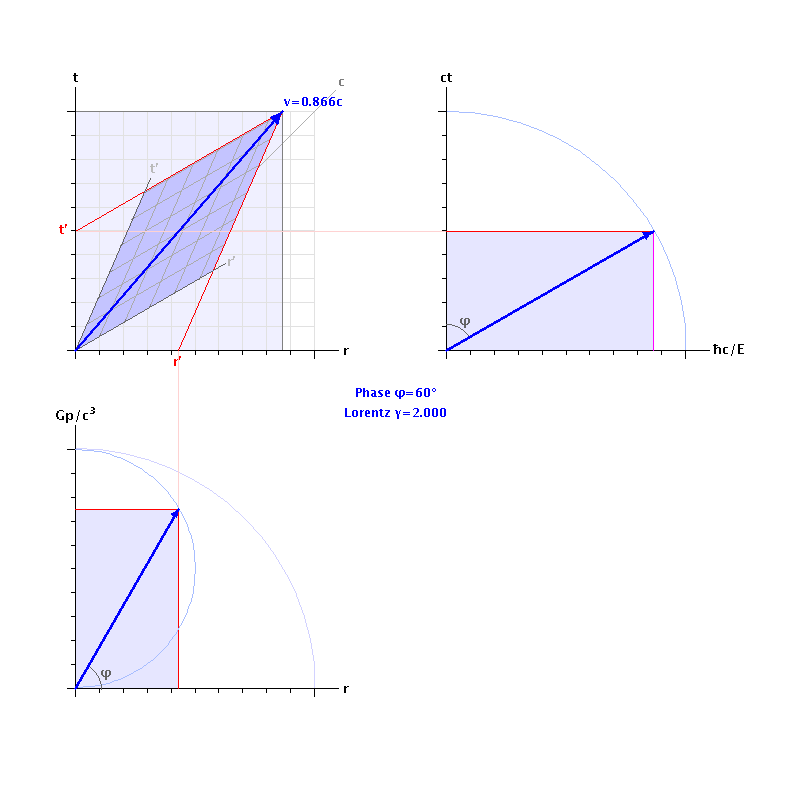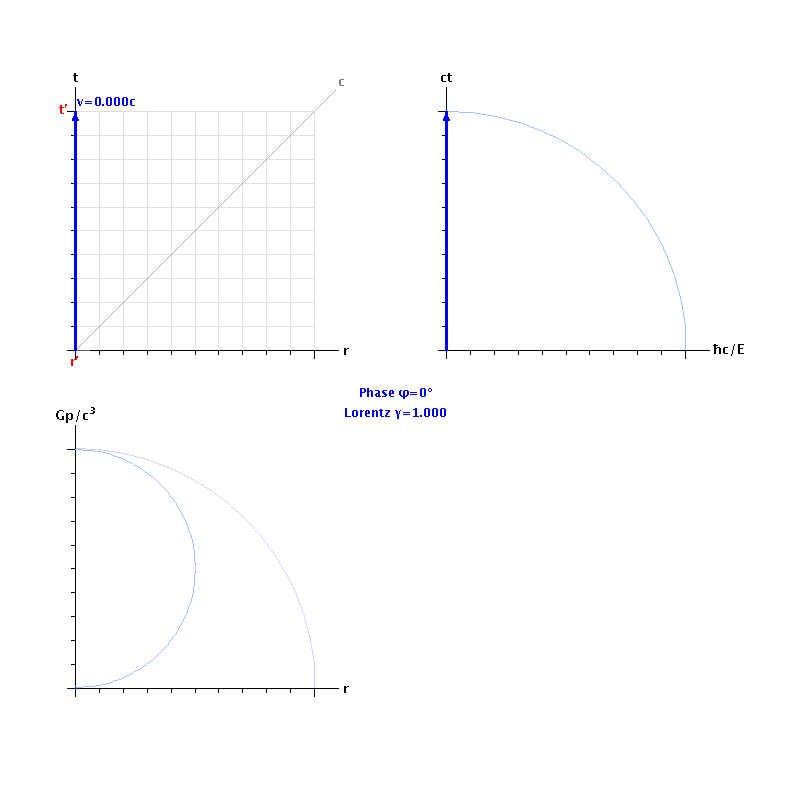
The top-right c3 projection shows the imaginary plane which couples (imaginary) time to the "Planck gauge" dimension, λ = ħ/mc. At light-speed, an observer in an inertial (rest) frame of reference observes the particle's clock stopping, as the moving frame reaches infinite time dilation. The potential energy of the particle's rest-mass becomes completely imaginary at this point. The vector's magnitude has Maxwellian dimensions of [L3/T2], corresponding to unitary mass or charge. The area enclosed under this mass vector has dimensions of [L3/T3], which corresponds to electrical current (charge moving in space) and rest-mass "flowing in time".
The bottom-left c4 projection shows momentum (kinetic energy) strongly coupled to space (the radial distance coordinate). At light-speed, real length contracts to zero, and the particle's momentum (p=mc) reaches unity on the Gp/c³ axis, so its kinetic energy is completely imaginary. The vector's magnitude has dimensions of [L4/T3], corresponding to units of momentum. The area enclosed under the momentum vector has dimensions of [L4/T4], i.e. force.
The bottom-right c5 projection shows the imaginary plane which couples the "Planck gauge" (potential energy) with the "Einstein gauge" (kinetic energy). The magnitude of the resultant vector is given by E² = (mcv)² + (mc²)², the particle's total energy, with Maxwellian dimensions of [L5/T4]. The area enclosed under this energy vector has dimensions of power, viz. [L5/T5].
Thus, the complex 5+1 dimensional framework is demonstrated as providing a simple yet robust mathematical model which elegantly correlates Maxwell's Units with Special Relativity, and with moving charge, i.e. Maxwell's electromagnetism. General relativity and loop quantum gravity are also naturally consistent with this 6D complex spacetime framework.